Introduction
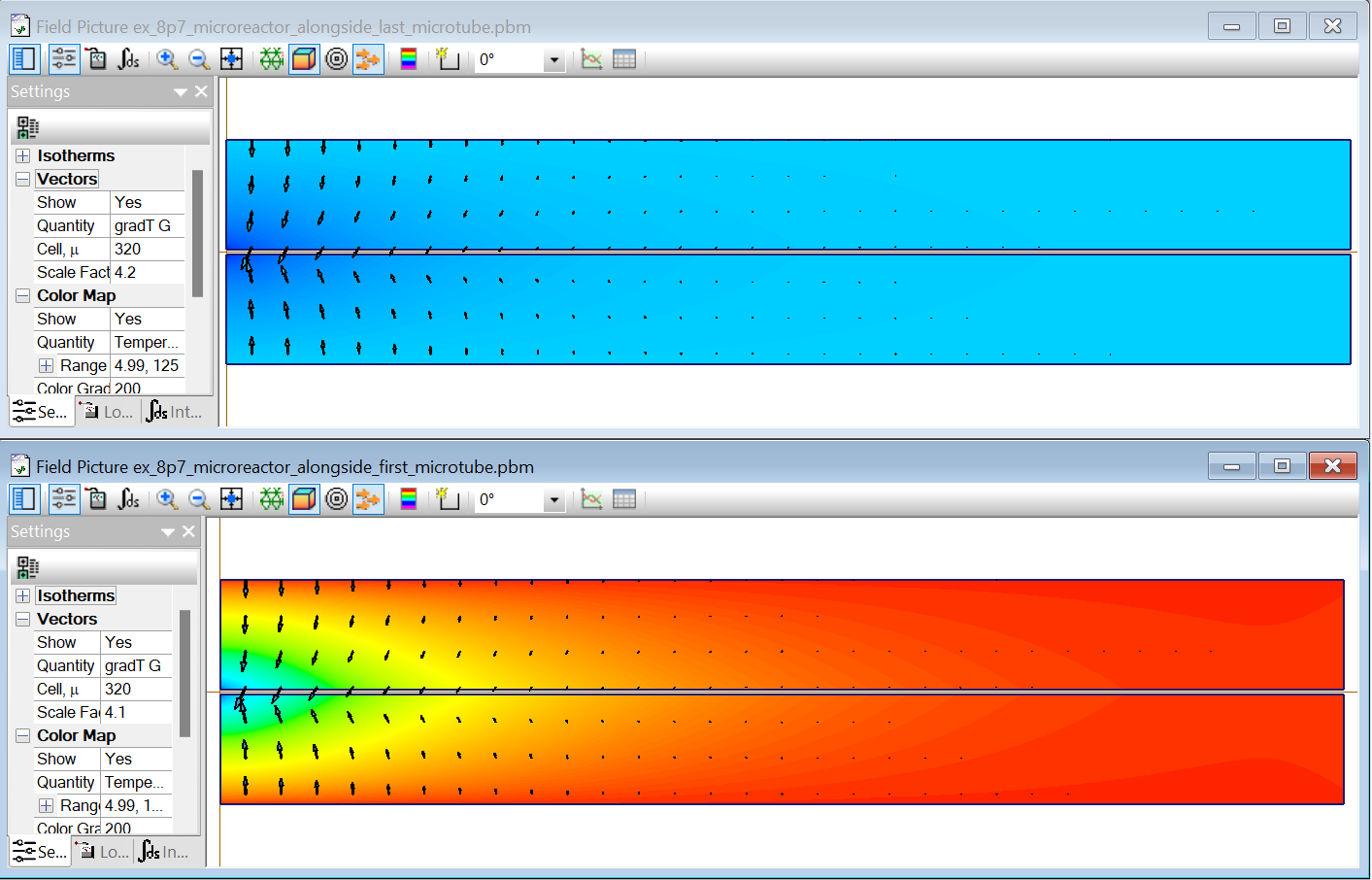
Le système est un microréacteur permettant d'étudier l'influence de la température sur
un microfluide. L'exercice original propose un microréacteur avec 100 microtubes
pour une étude tous les 1 degrès. Le modèle en utilise 50, réduisant de moitié la taille
du microréacteur en contrepartie d'une résolution de 2 degrès, mais aussi une meilleure
visualisation.
Par construction, on applique une température de 125 °C sur un côté parallèle
aux microtubes et 25 °C sur l'autre. La décroissance de la température étant linéaire,
le "pas" pour chaque microtube est de 2 °C.
-
Données d'entrée :
fluide : Tm,i = 5 °C (T. moyenne d'entrée)
fluide : Tm,o,1 = 124 °C (T. moyenne de sortie)
fluide : Tm,o,50 = 24 °C (T. moyenne de sortie)
fluide @ 288 K : k = 247.0e-3 W/m.K
: ρ = 1120.2 kg/m³
: Cp = 2359 J/kg.K
fluide @ 338 K : k = 261.0e-3 W/m.K
: ρ = 1085 kg/m³
: Cp = 2583 J/kg.K
dm : 4.56e-6 kg/s , débit massique moyen
Dh : 4ab/(a+b) = 64.0e-6 m , a = 160 μm, b = 40 μm
Dh : section hydraulique pour un microfluide
P : 2•(a+b) = 0.4e-3 m
-
Note : Une partie préliminaire de l'exemple démontre que le fluide
suit un écoulement laminaire en négligeant les turbulences de l'entrée.
Cela permet d'appliquer la relation suivante :
h = Nu•(k/Dh) avec Nu = 4.44.
Question / réponse (1/2)
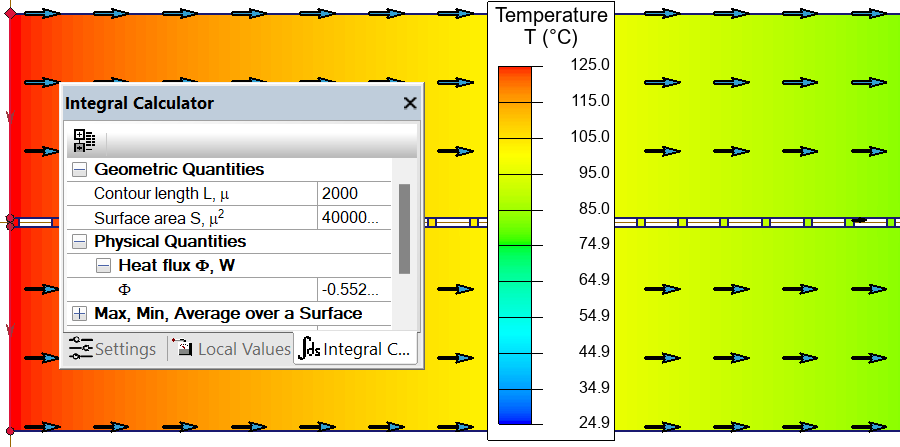
- Quelle est la puissance à réguler ?
- Réponse :
Les conditions limites sont définies comme dans schéma ci-dessous. Pour T0 de la condition de convection, on applique une loi linéaire décroissante.

Il suffit de définir un contour sur le côté à 125 °C et le calcul est fait automatiquement. P = 0.552 W.